
| Matematisk Fysik |  |
STATISTICAL PHYSICS OF COMPLEX SYSTEMSThomas GuhrHere, you find an introduction to my research interests. I discuss some projects and I also list my present collaborations. There are several recent articles which you can download. |
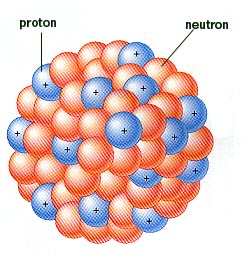
Quantum Chaos and Random Matrix ModelsRandom matrices provide powerful models for a rich variety of complex systems. Here is a brief overview.A good example is the atomic nucleus shown to the right. It consists of many nucleons, the protons (blue) and the neutrons (red). They all interact with each other and move in a very complicated way. Large parts of the quantum mechanical excitation spectrum have statistical features which are well described by assuming that the interaction matrix elements can be replaced by random numbers. One often refers to that as Quantum Chaos in nuclei. However, that is not the full story yet, because at some excitation energies, the nucleons move coherently. This leads, for example, to vibrations and rotations of the nucleus as a whole. Those collective excitations are not quantum chaotic. Hence, Random Matrix Models can be used to distinguish collective from quantum chaotic motion, to some extent even purely from the measured data. We analyzed experimental data of magnetic scissors mode excitations and of electric pygmy dipole excitations. In several different branches of physics, we study chaotically coupled systems or, equivalently, systems with symmetry breaking. The coupling or the symmetry breaking has a strong influence on the spectral statistics. In a recent work, we look at the time evolution of a certain energy localization effect which has been observed in coupled elastodynamical systems. Disordered systems are a wide field for applications of Random Matrix Models. Recently, we investigated a chaotic billiard with scatterers to study the interplay between chaos and disorder. local collaborator: Johan Grönqvist (PhD-student) external collaborators: Professor Achim Richter and his group at Technical University of Darmstadt, Professor Hans-Jürgen Stöckmann at University of Marburg. |
 |
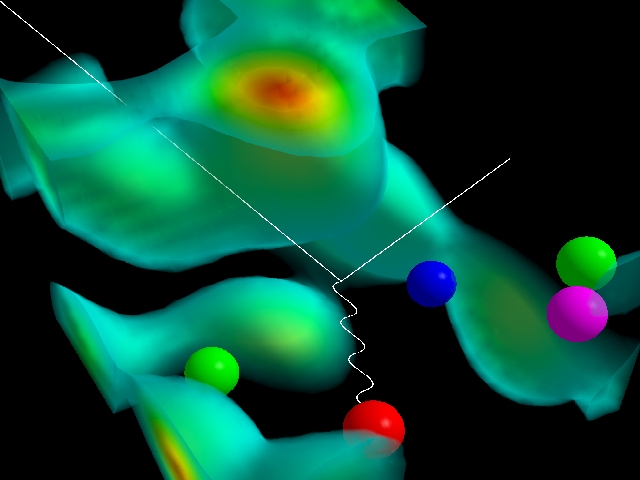
Courtesy of Derek Leinweber (CSSM) |
Quantum Chaos Approach to QCDQuantum Chromodynamics (QCD) is the theory of the strong interaction. The quarks (the colored spheres) interact by exchanging gluons which are discribed by gauge fields (the green clouds). Unfortunately, QCD is so involved that analytical calculations are only feasible after drastic approximations. Thus, one resorts to demanding numerical simulations, referred to as lattice gauge calculations. We contributed to the statistical analysis of those lattice data which show that QCD has much in common with disordered mesoscopic systems in condensed matter physics. But QCD is even more complicated, in particular due to chirality and chiral symmetry breaking. We setup an effective stochastic field theory. Presently, we investigate the motion of the quarks in individual gauge field configurations which matches the way how lattice gauge calculations are done. As a first step, we identified a hierarchy of semiclassical limits in QCD.local collaborator: Dr. Stefan Keppeler (Emmy Noether fellow) external collaborator: Professor Tilo Wettig at University of Regensburg. |
Supersymmetry and SupergroupsSupersymmetry became a prominent tool in the Theory of Random Matrices and Disordered Systems. I developed the Graded Eigenvalue Method as a new and exact technique to solve Random Matrix Models. In the course of doing so we were led to address the general problem of harmonic analysis on superspaces and, in this context, the theory of supergroups. Here is an introduction to the main ideas. We showed that certain matrix Bessel functions (in mathematics referred to as Gelfand's spherical functions) are kernels of diffusion equations which drive systems with arbitrary spectral correlations into the chaotic regime. We derived various new and explicit results beyond the unitary case for these diffusion kernels in ordinary and super spaces. As a side result, we also proved a supersymmetric generalization of Harish-Chandra's famous integral formula. These findings are conceptually important, but also useful for Random Matrix Theory. We found an unexpected connection between the building blocks of the correlation functions. We plan various further applications. Very recently, we considerably extended the Calogero-Sutherland models. We showed that supersymmetry yields, in a most natural way, models for two kinds of interacting particles which are likely to be exactly solvable.local collaborator: Johan Grönqvist (PhD-student) external collaborator: Dr. Heiner Kohler at University of Heidelberg |
|

Courtesy of Mark Oxborrow 
Courtesy of Lars Montelius |
Elasticity and NanomechanicsClassical wave phenomena are ubiquitous in technical applications. Quantum Chaos is the statistical theory of quantum waves. What can we learn from Quantum Chaos for classical wave phenomena? - We addressed this question by studying elastomechanical systems in a series of investigations over the years. This is non-trivial due to the presence of modes (pressure and shear) and due to the complicated boundary conditions. Among other things, we presented the first purely experimental and statistically highly significant study of parametric correlations. More recently, we showed that the elastic displacement field behaves statistically just like a quantum wave function. However, there is a beating phenomenon between the different modes. We now apply "semiclassical" ideas, that is, we study the ray limit of elastodynamics in which the wavelength is small compared to all system geometries. We hope to improve the understanding of elastodynamical spectra by relating fundamental features of those systems to geometric quantities of the ray limit. A first step was a Weyl approximation to the level density of the quartz sphere shown to the left. This is a monocrystal of grapefruit size whose spectra have been measured with fantastic precision.Little is known about the mechanical properties of systems on the micrometer and nanometer scale. An example is the cantilevers shown to the left. Nonlinear or chaos-related effects are needed to gain deeper insight into those systems. We wish to apply our knowledge of chaos theory and elastodynamics to the micrometer and nanometer scale. In particular, we are interested in micro-electro-mechanical systems (MEMS) and nano-electro-mechanical systems (NEMS) which are nowadays so important in engineering. We just finished our first project in collaboration with Professor Lars Montelius and his group here at the NanometerConsortium on elastic constants of those cantilevers. local collaborator: Dr. Niels Søndergaard (postdoc) external collaborators: Professor Clive Ellegaard, Mikkel Avlund at the Niels Bohr Institute, Copenhagen, Dr. Mark Oxborrow at the National Physics Laboratory, Teddington. |
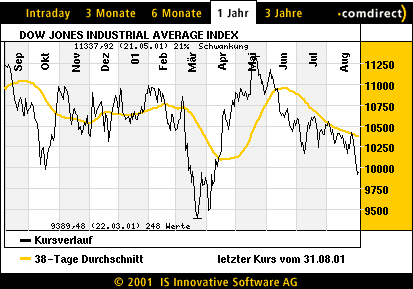
EconophysicsWhat is theoretical physics? - My definition is the following: Theoretical physics is construction and analysis of mathematical models for the quantitative description of reproducible experiments. These models ought to be as compatible as possible with each other to yield an ever more unifying picture for the measurable features of our world. - I cannot see any reason for myself to exclude biology, sociology or economics from the list of interesting research topics. On the contrary, I think that we physicists would make a big strategic mistake by confining ourselves to the more established topics and by leaving, for example, the quickly expanding field of mathematical modeling in economics to the mathematicians. The physicists' expertise, in particular the data- and experiment-oriented approach has a truly high potential in this field.The time series of stocks are correlated, because the performance of the corresponding companies is mutually connected. The measurement of those financial correlations is very important for risk managment. For various reasons, the empirically obtained correlations are dressed with noise. We developed methods to estimate and remove this noise, to begin with in a random matrix approach and then by inventing the power mapping as an alternative and supplement. We now study credit risk. Since an obligor can go bankrupt or default in another way, credits are risky for the banks that issue them. In turns out that the distributions of the losses are highly assymmetric and have long tails. A better quantitative understanding by means of improved models is crucial for the banks and a challenge for statistical physics. local collaborator: Dr. Rudi Schäfer (postdoc), Per-Johan Andersson, Andreas Öberg, Markus Sjölin, Andreas Sundin, Michal Wolanski, Patrik Frisk, Johnny Pégeot, Juan Manuel Vázquez Montejo, Fredrik Nilsson and Per Berseus (Examen-students) external contact: Dr. Axel Müller-Groeling (Pari-Group, Hamburg) |

 |